Definición:
Una función de dos variables tiene un máximo relativo en (a,b) si f(x,y)<f(a,b) cuando (x,y) esta cerca de (a,b).
El valor f(a,b) recibe el nombre de VALOR MÁXIMO RELATIVO
Si cumple que f(x,y)>f(a,b) cuando (x,y) esta cerca de (a,b) es un mínimo relativo en (a,b) y f(a,b) recibe el nombre de VALOR MÍNIMO RELATIVO
Si estas condiciones de desigualdad se cumple en todo el dominio de f(x,y) entonces toma el nombre de máximos y mínimos absolutos.
Suponga que las segundas derivadas parciales de f(x,y) existen y son continuas en un disco de centro (a,b) y suponga que fx(a,b)=0 y fy(a,b)=0 es decir (a,b) es un punto critico de f(x,y) sea:
Para Recordar:
*Máximos y Mínimos Absolutos
2
Si f es continua en un conjunto D cerrado y acotado en R entonces f alcanza un valor maximo absoluto f(x1,y1) y un valor minimo absoluto f(x2,y2) en algunos puntos (x1,y1)^(x2,y2) en D.
Para determinar los extremos absolutos:
1.- Calculan los valores de f en los puntos críticos de f en D.
2.- Se determinan los valores extremos de f en la frontera de D
3.- El valor mas grande es el máximo absoluto (Mabs) y el valor mas pequeño es el mínimo absoluto (mabs)
*Máximos y Mínimos Condicionados
Para determinar los valores extremos de f(x,y) sujeta a la restriccion g(x,y)=k(ecuacion de enlace) se procede a plantear a:


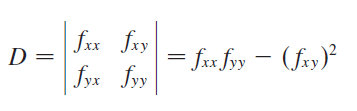







0 comentarios:
Publicar un comentario